# Задача малых поперечных колебаний струны
# Математическая составляющая
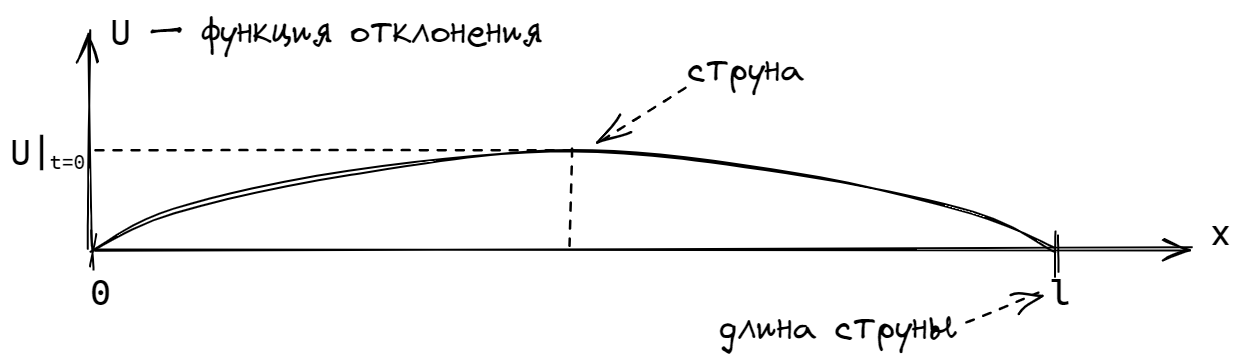
# Данные задачи
Уравнение малых свободных колебаний струны:
$$ \dfrac{\partial^{2} U}{\partial x^{2}}=\dfrac{1}{a^{2}} \dfrac{\partial^{2} U}{\partial t^{2}}. \tag{1} $$
Граничные условия:
$$ U|_{x=0;l}=0, \tag{2} $$
т. е. струна на концах жёстко закреплена и функция отклонения в этих точках равна 0.
Начальные условия (условия придания скорости струны в начальный момент времени):
$$ U|{t=0}=f(x); \quad \dfrac{\partial U}{\partial t}\bigg|{t=0}=F(x), \tag{3} $$
где $f(x)$ — функция, характеризующая степень натяжения, $F(x)$ — функция, характеризующая степень удара. Обычно одна из них берётся равной 0, так как ударить и натянуть струну одновременно достаточно проблематично.
# Метод Фурье
Для решения задачи используем метод Фурье (метод разделения переменных):
$$ U(x,t) = X(x)T(t). \tag{4} $$
Подставляем (4) в (1):
$$ \begin{align} X’’(x)T(t) &= \dfrac{1}{a^{2}}X(x)T’’(t); \quad | :X(x)T(t) \\\dfrac{X’’(x)}{X(x)} &= \dfrac{1}{a^{2}} \dfrac{T’’(t)}{T(t)}=-\lambda^{2}, \end{align} $$
где $\lambda^{2}$ — постоянная разделения. Рассматриваем каждое из уравнений отдельно:
$$ \begin{align} \dfrac{X’’(x)}{X(x)}+\lambda^{2}&=0; \quad | \times X(x) \\\dfrac{1}{a^{2}} \dfrac{T’’(t)}{T(t)}+\lambda^{2}&=0; \quad | \times T(t)a^{2} \\\\X’’(x)+\lambda^{2}X(x)&=0; \tag{5} \\T’’(t)+a^{2}\lambda^{2}T(t)&=0. \tag{6} \\\\\end{align} $$
Общее решение уравнений (5) и (6):
$$ \begin{align} X(x)&=c_{1}\cos(\lambda x)+c_{2}\sin(\lambda x); \tag{5.1} \\T(t)&=A\cos(\lambda at)+B\sin(\lambda at). \tag{6.1} \end{align} $$
Далее работаем с (5) и (5.1). Применяем граничные условия (2):
$$ X(0)=0; \quad X(l)=0. \tag{7} $$
Подставляем (7) в (5.1):
$$ \begin{align} c_{1}\cos(\lambda 0)+c_{2}\sin(\lambda 0) &= 0; \quad \to c_{1}=0; \\c_{1}\cos(\lambda l)+c_{2}\sin(\lambda l) &= 0; \quad \to \sin(\lambda l)=0; \\\lambda l&=\pi n; \\\lambda_{n}&=\dfrac{\pi n}{l}. \end{align} $$
Задача (5) с граничными условиями (7) — однородная краевая задача. Решается однородное дифференциальное уравнение (5) при однородных граничных условиях (7). Решение (5,7):
$$ \begin{align} \begin{cases} X_{n}(x)=c_{2}\sin\left( \dfrac{\pi nx}{l} \right); \tag{8} \\T_{n}(t)=A_{n}\cos\left( \dfrac{\pi nat}{l} \right)+B_{n}\sin\left( \dfrac{\pi nat}{l} \right). \end{cases} \end{align} $$
Получили систему линейных алгебраических уравнений (8) относительно неизвестных амплитудных коэффициентов. Коэффициент $c_{2}$ можно принять равным 1, так как он может быть любым и не представляет практического интереса. Согласно (4):
$$ U_{n}(x,t)=X_{n}(x)T_{n}(t). \tag{9} $$
Согласно методу Фурье, решение записывается в виде бесконечного ряда Фурье (дискретного спектра):
$$ \boxed{ \begin{align} U(x,t)&=\sum_{n=1}^{\infty}U_{n}(x,t) \\&=\sum_{n=1}^{\infty}\left( A_{n}\cos\left(\dfrac{\pi ant}{l}\right)+B_{n}\sin \underbrace{\left( \dfrac{\pi ant}{l}\right)}{\omega{n}} \right)\sin\left( \dfrac{\pi nx}{l} \right). \tag{10} \end{align} } $$
Далее ставится задача Штурма-Лиувилля, согласно которой уравнение (8) — собственная функция, а
$$ \lambda_{n}^{2}=\left( \dfrac{\pi n}{l} \right)^{2} $$
— собственное значение.
Уравнение (10) удовлетворяет граничным условиям (2), но не удовлетворяет начальному условию (3). Подставим (3) в (10):
$$ \begin{align} \begin{cases} f(x)=\sum_{n=1}^{\infty}A_{n}\sin\left( \dfrac{\pi nx}{l} \right); \\F(x)=\sum_{n=1}^{\infty}B_{n} \dfrac{\pi an}{l}\sin\left( \dfrac{\pi nx}{l} \right); \end{cases} \quad \bigg | \times \sin\left( \dfrac{\pi nx}{l} \right);\int_{0}^{1} , dx \tag{11} \end{align} $$
Смысл преобразований над системой (11): используя свойство ортогональности, производится домножение каждого уравнения на собственную функцию и интегрирование в пределах от 0 до 1. В результате получается бесконечная сумма из интегралов, но от всей этой суммы остаётся лишь одно слагаемое: при совпадении $n$ в сумме с $n$, на которое мы домножаем. Это слагаемое — ненулевой интеграл, который можно наблюдать в системе (12).
$$ \boxed{ \begin{align} \begin{cases} \displaystyle A_{n}=\dfrac{2}{l}\int_{0}^{l} f(x)\sin\left( \dfrac{\pi nx}{l} \right) , dx; \\\displaystyle B_{n}=\dfrac{2}{\pi na}\int_{0}^{l} F(x)\sin\left( \dfrac{\pi nx}{l} \right) , dx. \end{cases} \tag{12} \end{align} } $$
# Физическая трактовка решения
На рисунке изображены поперечные колебания струны.
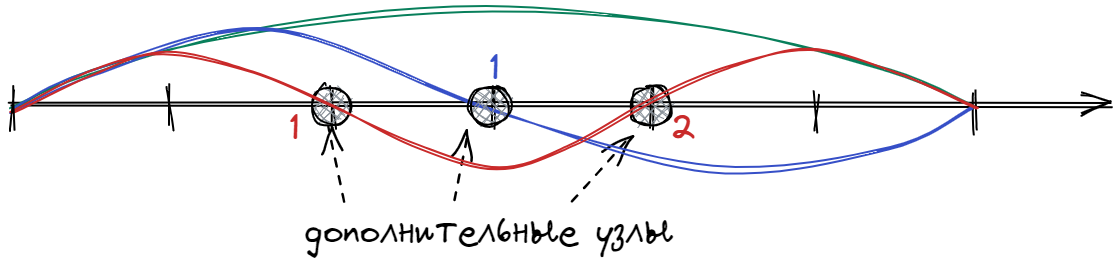
| Функция | Частота | Число полуволн синуса $n$ | Число доп. узлов |
|---|---|---|---|
| green | $\omega_{1}=\dfrac{\pi a}{l}$ | 1 | 0 |
| blue | $\omega_{2}=\dfrac{2\pi a}{l}$ | 2 | 1 |
| red | $\omega_{3}=\dfrac{3\pi a}{l}$ | 3 | 2 |
Частота $n$-ой функции, согласно (10), определяется формулой
$$ \omega_{n}=\dfrac{n\pi a}{l}, \tag{13} $$
где $l$ — длина струны.
Параметр $a$ определяется формулой
$$ a=\sqrt{\dfrac{\sigma}{\rho}}, \tag{14} $$
где $\sigma$ характеризует натяжение струны, $\rho$ — её толщину.
Частота колебания характеризует высоту его звучания. Зависимость прямая.
- Рассмотрим струну как физический объект музыкального инструмента, например гитары.
- Результирующее колебание называется тембром (набором частот), в котором преобладает основная гармоника. Все другие так же присутствуют, но с меньшими амплитудами.
- Струну можно натянуть:
- тогда изменится отвечающий за это параметр: $\uparrow\sigma$ и, согласно (13) и (14): $\uparrow a \quad \to \quad \uparrow\omega$, т. е. частота колебания увеличится, а следовательно, и высота его звучания.
- У струны можно ослабить натяжение:
- тогда: $\downarrow \sigma \quad \to \quad \downarrow a \quad \to \quad \downarrow \omega$, т. е. частота колебания уменьшится, а следовательно, и высота его звучания.
- Каждая из струн гитары имеет разную толщину (увеличивается от 1-ой к 6-ой).
- Тогда: $\rho_{6}>\rho_{1}; \quad \to \quad a_{6}<a_{1}; \quad \to \quad \omega_{6}<\omega_{1}$, т. е., согласно (13) и (14), частота колебания толстой струны 6 меньше частоты колебания тонкой струны 1, а следовательно, высота звучания толстой струны ниже, чем первой.
- Любую струну можно зажать на $n$-м ладу, тогда изменится её длина: $\downarrow l \quad \to \quad \uparrow\omega$, т. е., согласно (13), частота колебания увеличится, а следовательно, и высота его звучания.
# Физический смысл на примере гитарной струны, кратко
- $\uparrow \sigma \quad \to \quad \uparrow a \quad \to \quad \uparrow \omega$
- Натягивание струны приводит к увеличению частоты её колебания, что равносильно повышению высоты её звучания.
- $\downarrow \sigma \quad \to \quad \downarrow a \quad \to \quad \downarrow \omega$
- Ослабление натяжения струны приводит к уменьшению частоты её колебания, что равносильно понижению высоту её звучания.
- $\rho_{6}>\rho_{1} \quad \to \quad a_{6}<a_{1} \quad \to \quad \omega_{6}<\omega_{1}$
- Шестая струна толще первой, следовательно, коэффициент $a$ шестой струны меньше, чем у первой, следовательно, частота колебания шестой струны меньше, чем у первой, что равнозначно тому, что высота звучания шестой струны ниже, чем у первой.
- $\downarrow l \quad \to \quad \uparrow \omega$
- Зажатие струны приводит к уменьшению её длинны и к увеличению частоты её колебания (т. е. к повышению высоты звучания).