Last updated Unknown

• Ммпэд
• Электродинамика

• Решение дисперсионной задачи для П-образного волновода с применением МЧО.
• Есть 2 варианта разбиения поперечного сечения на частичные области.
  • Удачный.
  • Неудачный.
    • В этом случае в областях ни по горизонтальной оси, ни по вертикальной оси нельзя поставить задачу Штурма-Лиувилля.
      • Это приводит к записи решения в виде интеграла Фурье (непрерывного спектра), а не ряда Фурье (дискретного спектра).
        • Это весьма сложная с математической точки зрения процедура, которая приводит к интегральным уравнениям.
          • Если можно обойтись без использования непрерывного спектра, лучше это сделать.
• Записывается выражение для векторов Герца в виде бесконечной суммы (см. Метод Фурье).
• Записывается граничное условие для касательных к границам частичных областей составляющих компонент напряжённости электрического и магнитного полей.
• Компоненты поля выражаются через полученные продольные компоненты Векторов Герца.
• Согласно записанным граничным условиям, приравниваются на границе, получается система функциональных уравнений.
• Каждое уравнение системы, используя свойство ортогональности собственных функций, домножают на собственное значение и интегрируют в определенных пределах по $dx$, чтобы перейти к системе линейных алгебраических уравнений относительно неизвестных амплитудных коэффициентов.
• Записывается условие нетривиальности решения полученной однородной системы:
  • однородная система имеет нетривиальное решение (т. е. решение, отличное от нуля) в том случае, если её определитель равен нулю ($det=0$).
• Находим собственные функции и собственные значения.

• Правильность выполнения этой операции определяет корректность получаемых результатов.
• Основное требование:
  • обеспечение полноты систем собственных функций.
• Что будет, если неудачно разбить направляющую структуру на частичные области?
  • Может получиться так, что для некоторых областей нельзя будет сформулировать краевые задачи Штурма-Лиувилля.
    • Это приводит к записи решения в виде интеграла Фурье/непрерывного спектра (см. Преобразование Фурье), а не ряда Фурье/дискретного спектра.
      • Использование непрерывного спектра — весьма сложная с математической точки зрения процедура, которая приводит к интегральным уравнениям.
        • #π/следствие: если можно выбрать вариант разбиения на области, в которых не приходится иметь дело с непрерывным спектром, лучше это сделать.
• #π/следствие замены непрерывного спектра дискретным в случае неудачно разделения на частичные области:
  • нарушается условие полноты систем собственных функций;
    • #π/следствие:
      • потеря сходимости решения (см. Сходимость числового ряда);
        • Сходимость ряда Фурье так же можно понимать следующим образом: чем больше членов ряда Фурье мы учитываем, тем более точное решение мы получаем.
      • появление ложных нефизичных корней дисперсионного уравнения.

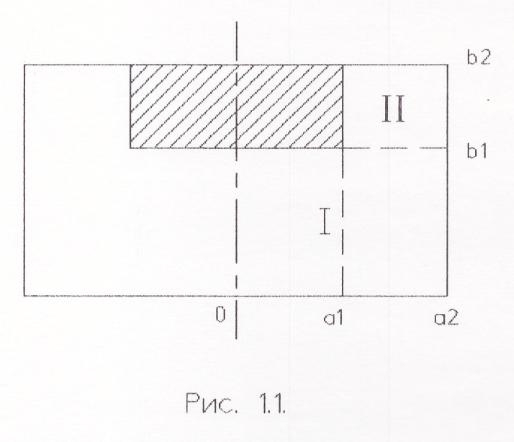
• На 2 области.
  • #π/иллюстрация:
    • 
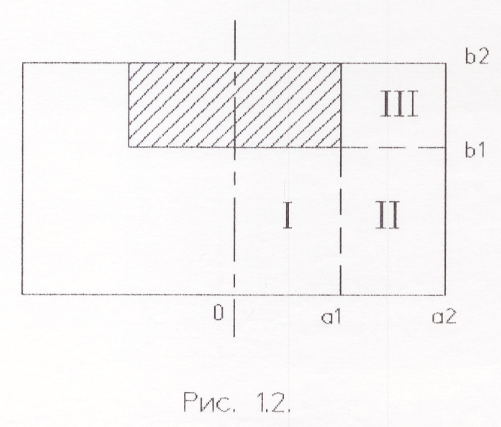
• На 3 области.
  • #π/иллюстрация:
    • 
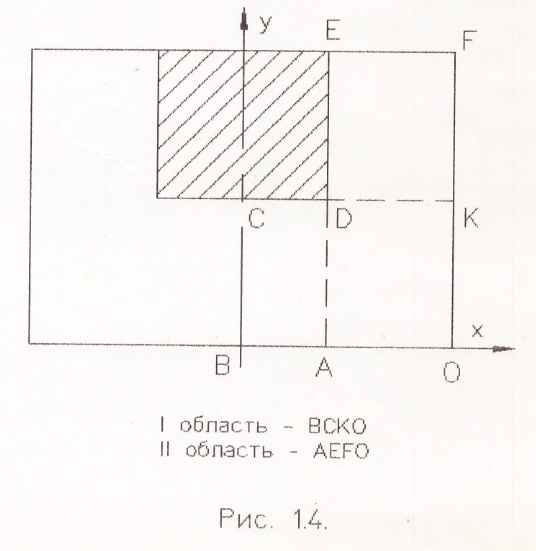
• На области с пересечением.
  • #π/иллюстрация:
    • 

• Берётся одна волна (основная квази-$H_{10}$, её волновое число;
• сходимость исследуется по кол-ву собственных функций, которые берутся в областях;
  • более конкретно: на графике зависимости критической длины основной квази-$H_{10}$ волны от числа учитываемых в выбранных областях собственных функций.
• делается вывод, сколько для обеспечения сходимости нужно взять этих функций.

• @MaystrenkoIssledovanieRaschyotSoglasuyushchih