Last updated Unknown

• Ммпэд
• Электродинамика

• Метод частичных областей — один из наиболее распространенных проекционных методов¹.
• #π/суть метода:
  • рассматриваемая электродинамическая структура подвергается декомпозиции – разбивается на отдельные частичные области, для каждой из которых формулируется краевая задача Штурма-Лиувилля на уравнениях Максвелла или на дифференциальных уравнениях, следующих из системы уравнений Максвелла.
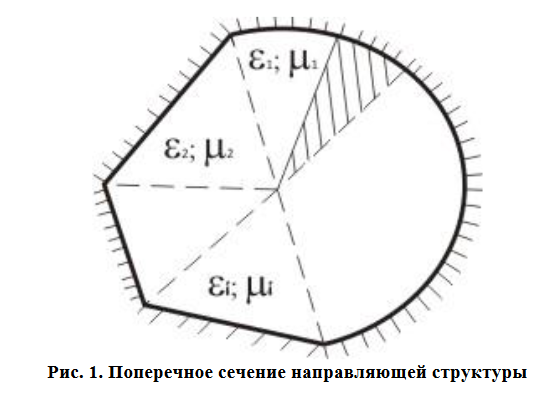
    • #π/иллюстрация:
      • 
    • Электромагнитное поле в каждой из выделенных областей представляется в виде разложений по собственным функциям указанных краевых задач.
      • Далее производится «сшивание» полей на границах между областями – приравнивание на границах между ними (областями) тангенциальных компонентов поля.
        • В результате получается система функциональных уравнений.
          • Использование условий ортогональности собственных функций краевых задач для выделенных областей приводит к системе линейных алгебраических уравнений относительно неизвестных коэффициентов разложения полей в частичных областях. Таким образом, метод частичных областей фактически является процедурой определения коэффициентов Фурье – разложений полей в декомпозированных электродинамических структурах. Базисы, которыми представляются поля в частичных областях, должны обладать свойством полноты на смежных границах этих областей, где производится проекционное сшивание тангенциальных компонентов полей $\vec{E^H}$ и $\vec{H^E}$, записанных в N-м приближении. При этом проецирование может производится как на базисы собственных функций скалярных краевых задач, образующихся в результате разделения переменных, так и на базисы векторных разложений полей. В последнем случае алгебраизация функциональных уравнений, получающихся из граничных условий, осуществляется на основе использования энергетических условий ортогональности. Этот вариант алгебраизации применяется, как правило, в дифракционных задачах для направляющих структур и при согласовании неоднородно заполненных частичных областей.

1. Поле в каждой из выделенных частичных областей обычно описывается продольными компонентами обоих векторов Герца.
2. Для каждого из координатных направлений можно выделить своё волновое число.
3. Тогда для каждой собственной функции имеет два поперечных волновых числа. Возможны 2 варианта:
   1. одно из поперечных волновых чисел определено в виде дискретного бесконечного набора чисел;
   2. оба они неизвестны и могут принимать любые значения в пределах от нуля до бесконечности.

• #π/причина перехода к непрерывному спектру:
  • в некоторых случаях поперечные волновые числа частичной области в направляющей структуре без потерь могут располагаться непрерывно в плоскостях значений $\alpha_{1,2}$, вдоль действительной и мнимой осей.
    • #π/следствие:
      • в этом случае полная система функций, образующих базис выделенной области, представляет собой непрерывный спектр.
• Предпосылки перехода к непрерывному спектру:
  • когда выделенная в результате декомпозиции направляющей структуры область:
    • либо не имеет границы, на которой выполняются условия, соответствующие задачи Штурма-Лиувилля;
    • либо такая граница есть и она может быть непрерывно продолжена в бесконечность.