# Определённый интеграл
- #π/определение с т. з. геометрии:
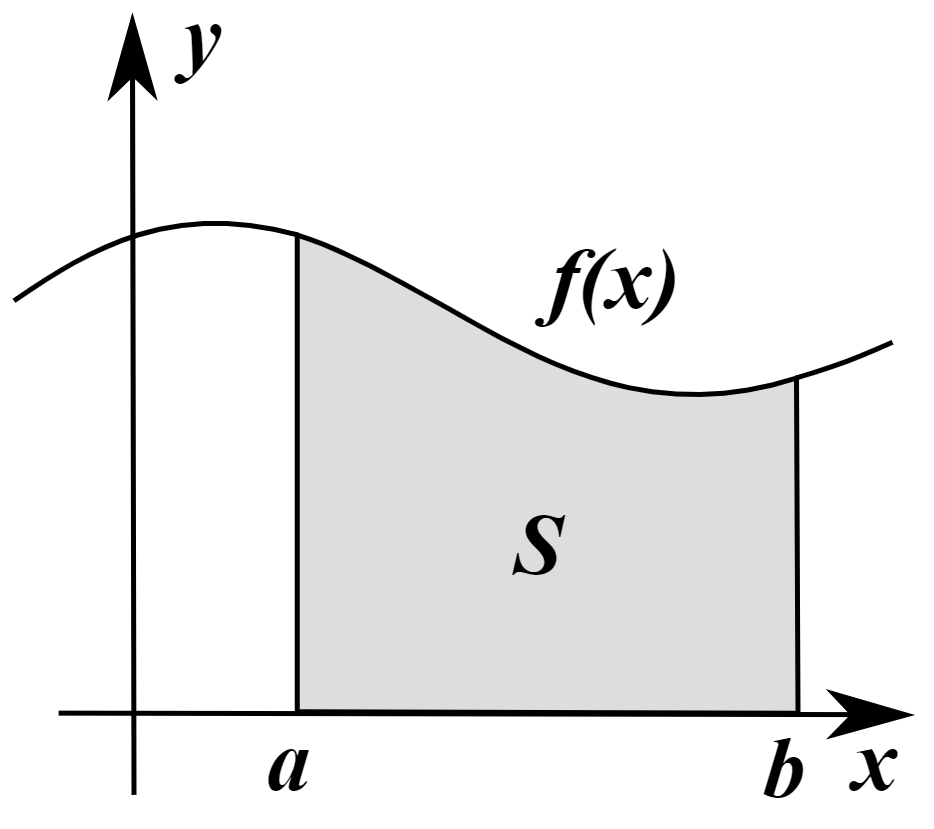
- Определённый интеграл — площадь «криволинейной трапеции», ограниченной графиком функции $f(x)$.
- #π/иллюстрация определённого интеграла как площади «криволинейной трапеции»:
- #π/иллюстрация определённого интеграла как площади «криволинейной трапеции»:
- Определённый интеграл — площадь «криволинейной трапеции», ограниченной графиком функции $f(x)$.
- #π/определение (полное):
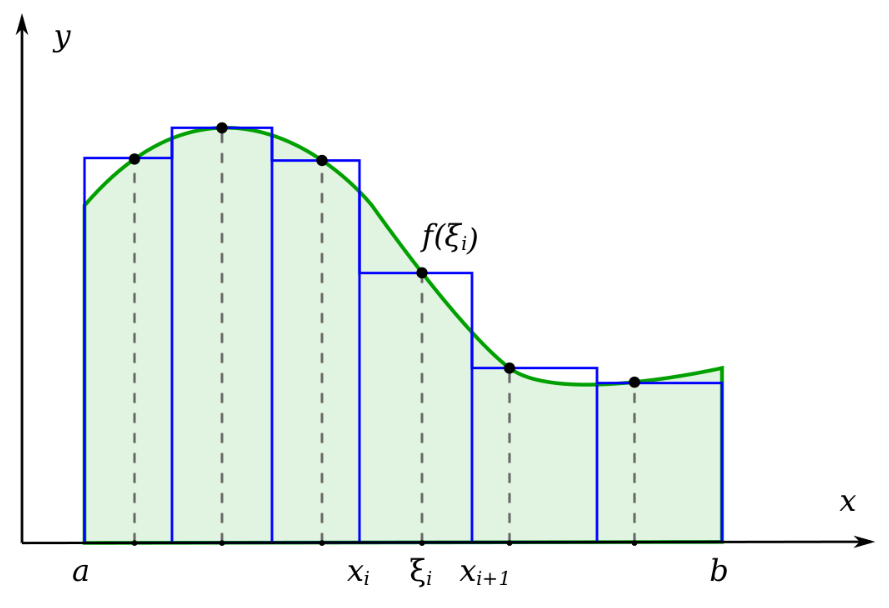
- Определённый интеграл функции $f(x)$ по промежутку $[a;b]$ — конечный предел интегральной суммы $\displaystyle \sum_{i=0}^{n-1}f(\xi_{i})\Delta x_{i}$ при $n \to \infty$, не зависящий ни от способа дробления отрезка $[a;b]$, ни от выбора точек $\xi_{i}$.
- #π/формула:
- $\displaystyle \int_{a}^{b} f(x) , dx = \lim_{\Delta x \to 0} \sum_{i=0}^{n-1} f(\xi_{i})\Delta x_{i}$, где:
- $f(x)$ — подынтегральная функция;
- $\Delta x_{i}=x_{i+1}-x_{i}$ — длина частичного отрезка;
- $f(\xi_{i})$ — значение функции в точки $\xi_{i}$;
- $n$ — кол-во частичных промежутков отрезка $[a;b]$.
- $\displaystyle \int_{a}^{b} f(x) , dx = \lim_{\Delta x \to 0} \sum_{i=0}^{n-1} f(\xi_{i})\Delta x_{i}$, где:
- #π/иллюстрация:
# Формула Ньютона-Лейбница
- На практике для вычисления определённого интеграла используется Формула Ньютона-Лейбница.
- #π/причина:
- трудности применения описанной выше формулы на практике, даже для простых функций.
- #π/причина:
- #π/формула Ньютона-Лейбница имеет след. вид:
- $\displaystyle \int_{a}^{b} f(x) , dx = F(b)-F(a)=F(x) \bigg|_{a}^{b}$.
# Алгоритм решения определённого интеграла
- Сначала находим первообразную функцию $F(x)$ (неопределенный интеграл).
- Константа $C$ в определенном интеграле не добавляется.
- Подставляем значение верхнего предела в первообразную функцию: $F(b)$.
- Подставляем значение нижнего предела в первообразную функцию: $F(a)$.
- Рассчитываем разность $F(b)-F(a)$, то есть, находим число.