# Производная функции
- #π/определение:
- Производная функции в точке — предел отношения приращения функции $\Delta y$ к вызвавшему его приращению аргумента $\Delta x$ в этой точке при $\Delta x → 0$1.
- #π/формула:
- $\lim_{\Delta x \to 0} \dfrac{\Delta y}{\Delta x}$.
- #π/иллюстрация:
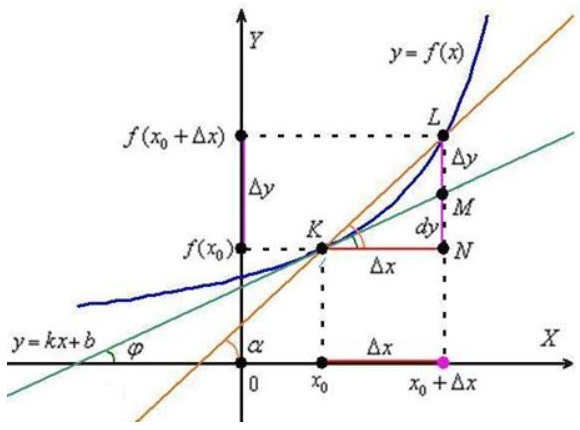
- Отрезок $NM$ — это дифференциал $dy$ приращения функции $\Delta y$.
# Физический смысл производной
- #π/суть:
- Производная функции показывает скорость её изменения в определённой точке.
- #π/иллюстрация физического смысла производной:
# Пример производной в жизни
- Спидометр в автомобиле показывает производную нашего перемещения2.
# Геометрический смысл производной
- #π/иллюстрация геометрического смысла производной:
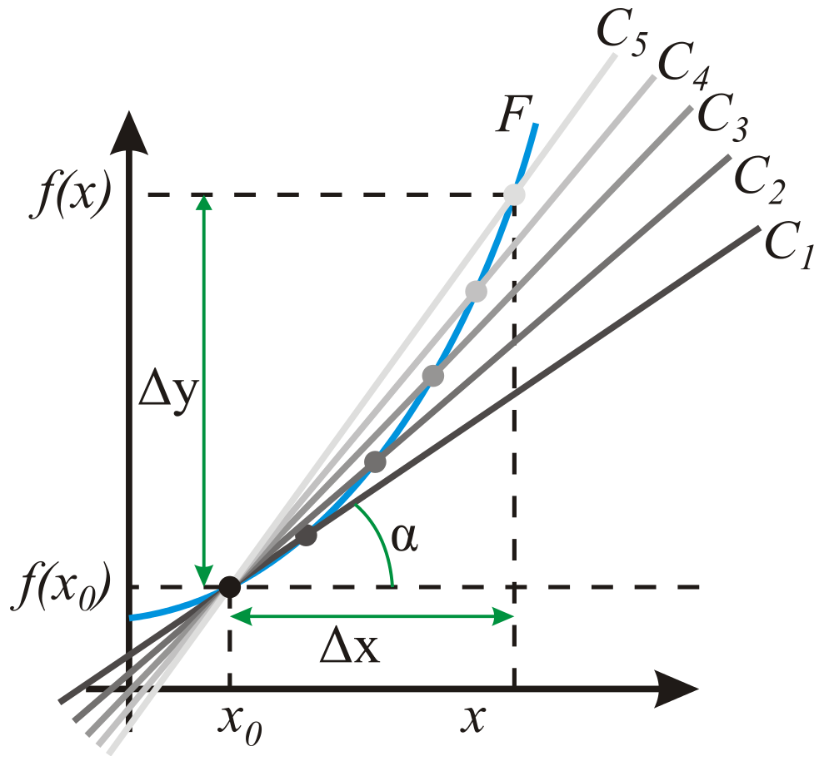
- На графике функции выбирается абсцисса $x_0$ и вычисляется соответствующая ордината $f(x_{0})$.
- В окрестности точки $x_0$ выбирается произвольная точка $x$.
- Через соответствующие точки на графике функции $F$ проводится секущая (первая светло-серая линия $C_{5}$).
- Расстояние $\Delta x = x - x_{0}$ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии $C_{5} — C_{1}$).
- Тангенс угла $\alpha$ наклона этой касательной — и есть производная в точке $x_0$.
# Аналогия с дорогой
- Хорошая аналогия для понимания производной — рассмотреть некоторую функцию и представить, что это дорога, на которую смотрят сбоку1.
- Дорога эта холмистая, но прямая, без возможности свернуть влево/вправо.
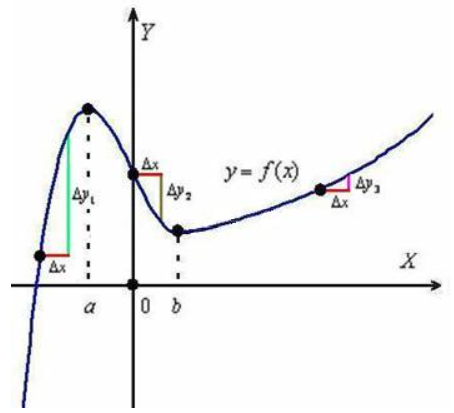
- Мы идём слева направо, каждый раз проходя одинаковое расстояние относительно оси $x$, которое обозначается как $\Delta x$ и является приращением аргумента.
- Оно в свою очередь вызывает приращение функции $\Delta y$.
- Отношение $\dfrac{\Delta y}{\Delta x}$ показывает среднюю скорость изменения функции.
- Оно в свою очередь вызывает приращение функции $\Delta y$.
- #π/иллюстрация:
.gif)