Last updated Unknown

• Ммпэд
• Электродинамика

• Уравнения Максвелла в $\int$-ой и $d$-ой форме описывают все электромагнитные явления и верны всегда.
  • Уравнения в $\int$-ой форме не являются локальными (то есть они не соединяют величины в конкретной точке пространства).
  • Уравнения в $d$-ой форме являются локальными, но при переходе от $\int$-ой и $d$-ой форме накладываются ограничения: функции должны быть дифференцируемы.
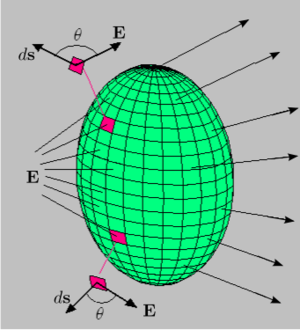
  • #π/иллюстрация потока э/м поля через замкнутую поверхность:
    • 

• Теорема о циркуляции магнитного поля
• Закон индукции Фарадея
• Обобщённый закон Кулона
• Закон Гаусса для магнитного поля

• #π/иллюстрация:
  • 
    1. Описывает все опытные данные о МП;
    2. Математическая форма закона ЭМ индукции Фарадея;
    3. Обобщённый закон Кулона;
    4. Отражает опытный факт об отсутствии в природе свободных магнитных зарядов.

1. Линейность
   • Принцип аддитивности. Как следствие - принцип суперпозиций.
2. Инвариантность
   • Инвариантность уравнения Максвелла есть обратимость процессов - она имеет место быть лишь при сохранении ЭМ энергии, когда она не переходит в другие виды энергии.
3. Симметричность
   • Если проводимость среды равна 0, и если заменить Е на Н и -эпс на мю, то мы получим такие же уравнения. Если ПС не равна нулю, то уравнения можно симметрировать искусственно, введя магнитные токи и заряды.